The cdf of X is given by
where
being
-f1SEp(≈0 =
(τ⅛∙) g(kx)
for X < 0,
for X > 0,
1 - (ττ⅛λ) G(-)
1 1 + « 2 J V ft /
for x < 0,
for x > 0,
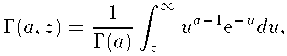
a > 0, z > 0,
the regularized gamma function. G is the cdf of the symmetric exponential power
distribution with zero mean and unit variance obtained when к = 1.
The momemts of order r, r = 1, 2,..., of the SEP distribution are:
E(Xr) =
If 0 ∈ IR is a position parameter and φ > 0 is a scale parameter, then it is possible
to bring back the three distributions to be characterized by four parameters using the
transformation Y = θ + φX. Moreover, the skewness and kurtosis indices can be easily
obtained relating moments from the origin and central moments.
3.2 The experiment
Here we show the results of the Monte Carlo experiment run to interpret the association
parameters of the (5) when the marginals are the three distributions seen above. Ac-
cording to the instruction given in Koehler and Symanowski (1995) samples are taken
from a three-dimensional KS distribution for different values of α12, αl3, '∣2.i and setting
α11 = <∣22 = «33 = 0. For each sample the correlation coefficient as a measure for the
linear relation and the Kendall’s coefficient for the monotone relation are calculated for
all pairs of variables. Table 1 shows the results for samples of size n = 50000, where
the marginals have zero mean, unit variance and, respectively, skewness equal to -0.5,
0, 0.5 and kurtosis equal to 5, 6, 8.
To comment the results, note that changing the values of the association parameters
we obtain very different dependence measures, but no particular links among them can
be pointed out. Moreover, it seems that marginal have not a big effect on the dependence
structure of the KS distribution, because the values of the correlation coefficients and
Kendall’s taus do not vary a lot in the three cases we have studied.
4 Fitting the KS distributions to data
4.1 Data
The raw data used in this paper are weekly prices of four market indices: the SfeP
500 Composite index (SfePCOMP), NASDAQ Composite index (NASCOMP), NIKKEI
500 index (JAPA500) and MSCI AC World index (MSACWFL). The observations have
been obtained by Datastream for the period 1/1/1988 to 12/31/2003. Then, we have
computed the returns as first differences of the natural logarithm of each series, rt =