The name is absent

form that also take into account negative correlations can be obtained by applying the
transformation ½ = 1 — Ui to some, but not all, variables (other characteristics of the
KS formulation can be found in Caputo, 1998; Manomaiphiboon, K. and Russel, A.G.,
2003).

We can obtain also specific marginal distributions of (3) by applying the inverse
probability transforms to Ui- Let the random variables Xi, i = 1, 2,... ,p, have cdf Fi
with corresponding inverse F~¹ and pdf fa. Then, the Xi = Ffa¹(Ui) have joint cdf

P           P

F(x₁,x₂,...,x_p) = ∩F_i(₁,) ɪɪ Cfa_j^a'^j,                  (5)

∙≈ = 1          _ιj=ι'+l

and pdf

Pl       P      ∖

f(x₁,x₂,...,x_p) = JJ I fi(xi)D_i ɪɪ C~^a'¹ I
i=l ∖           j=ij-l        /

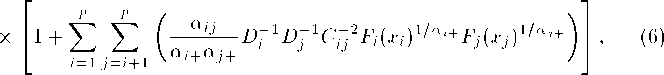
where

p

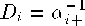
an + y^(.aikF_k(xk)^lfak+C~_k¹)
k≠i

and, in this case,

C_ij = F_i(x_iγ∣^a^ ₊ Fj-(¾)¹∕^α⅛ _ _jp.^.)l∕α._{+ j}p^_a.^l∕α_j+j

where the ɑʊ parameters assumes the meaning seen before. It is immediate to verify
that, in order to simulate the joint distribution of ɪɪ, X₂,..., X_p with the Monte Carlo
method, it is sufficient to generate some variates using (4) and then apply the inverse
transformation to each marginal.

3 Monte Carlo study

In this section we present the results of a Monte Carlo study on the dependence structure
of the KS distribution with skewed, fatted tails risks. The results of simulations and
of the application shown in the next section have been obtained using a FORTRAN
90 code implemented on a 2300 MHz PC Intel on Windows 2000. The code uses the
random number generator and the optimization routines of the NAG Fortran library.

3.1 KS Marginals

The Monte Carlo experiment has been run using as data generator process the skewed
Student t, generalized secant hyperbolic and exponential power (generalized error) dis-
tributions, which are useful in financial risk analysis because have heavier tails than the
normal distribution.

Since in their principal definition these distributions are symmetric, to skew them
we have followed Fernandéz and Steel (1998), who have introduced skewness in a sym-
metric distribution adding inverse scale factors in positive and negative orthants. More
precisely, if g is a symmetric pdf on zero with support IR, then for any к > 0 we obtain
a skew density

/ о ∖

/(«) ⁼ ( T~L ) 9(n~^Sën{x}x).

∖ ɪ K /

<<   1   2   3   4   5   6   >>

More intriguing information