We can write the cdf F and the quantile function F~1 corresponding to a skew
density f of an X distribution using the cdf G and the quantile function G~1 of the
symmetric density. We have
F(x) =
for X < 0,
for X > 0.
for the cdf and
f ⅛G^1 [(1 + κ2)⅞] for x < 0,
F~1(x) = < L 2J ~
ɪ-κG~1 [(1 + κ-2)++ for x > 0,
for the quantile function. Moreover, the moments of order r, r = 1, 2,..., can be written
as
/.'r÷ ' 4- (~ ŋ
E(Xr) = 2E+(Xr)-------K~(r+1) ,
κ + ∑
where oo
E+(Xr) = / xrg(x)dx
Jo
is the r-th moment of the symmetric distribution truncated to positive values. Clearly
E+(Xr) assumes the value of the r-th moment of the symmetric distribution divided
by 2 when r is even.
On the basis of these formulations, we present the main characteristics of the dis-
tributions considered (for details see, among others, Ayebo and Kozubowski, 2003;
Lambert and Laurent, 2001; Palmitesta and Provasi, 2004).
Skew Student-t. A random variable X has a skew Student t distribution (SST) if the
parameters к > 0 and v > 2 exist such that the pdf of X is
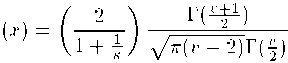
2s8nC)κ2'
(v÷l)∕2
where Γ(∙) indicates the gamma fucntion. If к = 1, the distribution is symmetric on
zero and has zero mean and unit variance. The cdf of X is given by
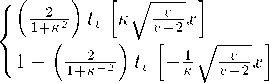
for x < 0,
for x > 0,
Γ(4±l) / 2∖- C + l)∕2
where
Tsst(«) =
t+)= ЛгД ι+- dw
J-00 √≡Γ(+ V V J
is the cdf of the unsealed Student t with υ degrees of freedom.
The moments of order r, r = 1, 2,..., of the SST distribution are:
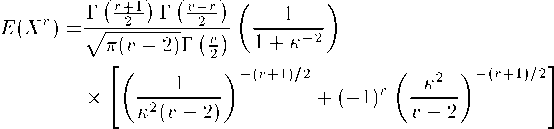
and exist when v > r.