Notes on an Endogenous Growth Model with two Capital Stocks II: The Stochastic Case

change of wealth with respect to human capital. The first weight is the marginal product
of human capital in goods production, given a certain choice of ut . The second weight is
the potential marginal product of human capital when the remaining fraction of human
capital is allocated to the educational sector.

We now turn to the Euler Equations. The envelope property with respect to physical
capital is straightforward. Together with the above first-order necessary conditions (15)
and (16), it gives rise to the following Euler equation in consumption:

ɪ = βEt Γ ɪ αy^t+1l .                          (17)

ct        ^t ct+1 kt+1

This is the Lucas asset pricing equation (cf. Lucas, 1978) with the constant of relative
risk aversion being equal to one. Along the optimal consumption path, marginal utility
of consumption in time t must be equal to the discounted expected marginal utility from
the return on investment in the next period. The envelope condition for the stock of
human capital is given by:

∂V^t = βEt Γ∂V^t+1 B(^1-α+γu^t) 1 .                            (18)

∂ht      ^t ∂ht+1    1-α

The last term on the right-hand side, γut , indicates that the expected marginal social
gain of exploiting the external effect in goods production has an impact on the evolution
of the shadow price of human capital. To be precise, today’s shadow price of human
capital is positively influenced by the degree of the external effect of human capital in
goods production. This is the mechanism by which the external effect enters the second
Euler equation along the optimal allocation of human capital between the two sectors:

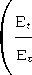
1
_           ∖ α

ɪ I (1-α)At ʌ ,
ct+1 kt+1 J^{v t} I __k

(^1-α+Yut+1)yt+1 1 B I    h —,

^ct + 1ht + 1^ut + 1 J / ht

(19)

The transversality conditions with respect to the two capital stocks that establish the
sufficiency of the two Euler equations (17) and (19) are given by:

lim β^τE₀ Γ^αyT-k_T 1 =0 and lim βTE₀ Γ(^1-α+γu,^τ)^yτ h_T 1 =0.       (20)

T→∞   ^{0 cT kT T}           T→∞   ^{0   cTuT hT   T}

The conditions (20) assert that the intertemporal budget constraints are met by the
planner’s decisions. Since the social planner exploits the external effect of human capital,
the derivative of the production function with respect to human capital looks different
from that in a decentralized economy below. This derivative is the sum of the private
marginal return from ut ht and the marginal social gain of the average stock of human
capital ht.

Using the guess and verify method, it is possible to generalize Robinson Crusoe’s
value function V and the planer’s value function found in Bethmann (2002) as follows:

V =θ+θBlnB+θAlnAt+θklnkt+θhlnht,                (21)

where the θi ’s, with i ∈ {k, h, B, A}, are defined as follows²:

_θ  ._   (^1-α+^γ)^β      _д ______¹______ θ       ^α      θ ___^1-α+Y__

^θB :   (1-β)²(1-αβ) ^{,   θ}A :   (1-ρβ)(1-αβ) ^, θ^k :   1-αβ^,   θ^h :   (1-αβ)(1-β) ^.

2The constant term is p-i_ven bv: θ — ^ln[^1-αβ] ₊ (^1-α) lⁿ[^1-β] ₊     ^αβ l^{n α}    + (1^-αβ+γ) ln^β +

lne constant term Is given b^y: ^θ :=   i-β   + (i-β)(i-αβ) + (1-β)(1-αβ) + (1-β)²(1-αβ) +

(1-α) ln[1-α] . β(1-α+γ) ln[1-α+γ]    (1-α + βγ) ln[1-α+βγ]

(1-αβ)(1-β) ⁺     (1-αβ)(1-β)²            (1-αβ)(1-β)²     '

<<   4   5   6   7   8   9   10   >>

More intriguing information