Testing the Information Matrix Equality with Robust Estimators

To simplify the notations and calculations that follow we transform M in
order to diagonalise V .Let

1+d 0 -d

W=  010,

-101

where

Eφ [(u⁴ - 6u² + 3)(u² - 1 - 2IF)] _ 1    1    ₍ 4

Eφ ((u⁴ - 6u² + 3)2)       = 2 - 12 E^φ u

Then

1

WM = —
σ²

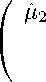
- 1 - d(μ₄ - 6μ₂ + 3)
ʌ        O .ʌ

^μ3 ^{- 3μ}1

^μ4 — 6 ^μ2 + 3

1 / u² - 1 - 2IF (u; σ; Φ) - d (u⁴ - 6u² + 3) ʌ

Wξ ( Y ; θ ) = -2                  u³ - 3 u                  ,

^σ               u⁴ - 6u² +3

and V = WVW' is given by

1
V = σ4diag[A, 6, 24],

where

A = -8 + 4ASV(^) + 2E (u⁴IF) - 1 [E (u⁴IF)]² .        (10)

We conclude that the IM test statistic in the normal model can be written
as the sum of three (asymptotically independent) statistics,

A^{+ (μ}2 ^{- 1 - d(μ}4 ^{- 6μ}2 ^{+ 3))}2 ⁺ 6^(μ3 ^{- 3μ}1)²

⁺ 24^(μ4 ^{- 6μ}2 ^{+ 3)2} .

<<   6   7   8   9   10   11   12   >>

More intriguing information