The name is absent

PEDRO PABLO ALVAREZ LOIS

with

(2.3)

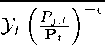
The variable Vjχ determines the critical value of the productivity parameter
Vj,t for which the unconstrained demand equals the supply constraint l},_t. The
term (Fj._t∕P_t)^-6 appearing in the demand function of a firm with excess capacities
represents, at given >'_t, the positive spillover effects a firm with idle resources
benefits from. As mentioned above, for tractability purposes I shall assume that all
intermediate firms are ex-ante equal. This symmetry means that input prices and
capacities are the same across firms. Assuming that a law of large numbers applies
in the present context, the final output supply can be expressed as follows
(2.4)

y_t

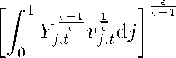
or taking into account equation (2.2),

y_t

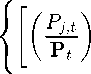
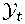
/ t>dF (t>) + l_t ^e

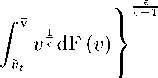
Recall that F(t>) is the distribution function of idiosyncratic shocks; thus, for a pro-
portion F(v) of intermediate firms, the realized value of the productivity parameter
is below v. Some manipulation of the previous expression allows one to write rela-
tive prices as a function of ¾, the proportion of firms with excess capacities

1

Z                                    .-.               λ ^e-1

.    .                    Ptt t ^t . . .       ≤≡L Γ I . .

(2.6)            -ɪ = < / t>dF (t>) + υ_t ^e / v≈dF(v)? -

Pt [√v                 Jvt          J

The right hand side of this expression is increasing in υ and bounded above by
1. To see this, first notice that the marginal productivity of a supply-constrained
input, ∂yt∕∂Yj,t, remains larger that its marginal cost, Pj._t, while they are equal
for unconstrained inputs. Thus, in the case that some input is supply-constrained,
one obtains that

f¹ 8Vt           f¹

(2.7)                   y_t = J,              > J_o Pj,tYj,t.dj

where the first equality is achieved by applying the Euler Theorem. The price of
the final good is equal to the shadow price index for intermediate inputs, which is
computed by using the marginal productivities of inputs in the production of final
output, that is,
where the price-index expression is obtained from the maximization problem of
the final-good firm. Notice that when no supply constraints are binding, υ -÷v,
the model shrinks to the standard case and ∂yt∕∂Yj,t = Pj,t- In such a case, the
symmetric equilibrium relative price of an intermediate good with respect to the
final good, PjxJYt, is equal to one. Moreover, under these circumstances, the

<<   3   4   5   6   7   8   9   >>

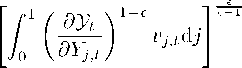
More intriguing information