Testing for One-Factor Models versus Stochastic Volatility Models

= 2

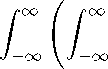
1 _{|_M__a|_<g_n_}CT⁴(u)Lχ(r, u)du
^f∞∞ ¹ {∣u-_a∣<ξ_n}LX ⁽¹^,u^)d^u

Lχ(r, a)da + θa.s.(1)

= 2

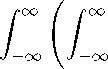
a.s. 2

¹ {∣zξn∣<ξn}^σ⁴⁽^a⁺^zξn ) ^LX ⁽^{r, a}⁺^zξn ^)d^z^f∞∞ ¹ {∣zξ_n∣<ξ_n}LX⁽¹^{, a}⁺^zξn^)d^z

Lχ(r, a)da + o_a,_s. (1)

Proof of Step 4:

Z∞

-∞

Lχ(r, a)²MM d ^a.

(20)

^Cn,r

₁ L (ⁿ^_¹) ^rJ

l σ ²( Xs )d s
0

√= £ ^σ²⁽^Xi/n) ^--n
V ⁿi =1

₁ ^l⁽ⁿ^_¹)^r^J^l⁽ⁿ^_¹)^r^J ∕∙( i+1) /n

-= £ σ²(Xi/n) -√n £ I σ²(Xs)ds

nⁿ i =1 i =1 ^7i/n

^l⁽ⁿ^_¹)^r^J _r( i+1) /n

n £

i=1 ^i/n

(σ ²( Xi/n )

- σ²(Xs)) ds

(21)

and, given the Lipschitz assumption on σ²(∙), the last line in (21) is o_P(1) by the same
argument as the one used in Step 1.

Given Steps 1-4 above, it follows that the quadratic variation process of Z_n,_r is given by

2 [∞ σ⁴ (a) Lx(r, a)da + 2 [∞ σ⁴ (a) L^χ⁽^ a).2 da - 4 [∞ σ⁴ (a) L^χ⁽^ a).2 da

-∞ -∞ LX (1, a) _-

∞ LX (1, a)

= 2 [∞ σ⁴ (a) L^χ⁽^r, a⁾⁽LX⁽1^,a) - L^χ⁽^r, a)) da. (22)

∞ -QQ ^LX ⁽¹ ,a)

The statement in the theorem then follows.

(i)b Without loss of generality, suppose that r < r'. By noting that

1 ^l⁽ⁿ^_¹)^r^J^l⁽ⁿ^_¹)^r^J

-= £ sn (Xi/n ) -√n £ (Xi+1 /n - Xi/n )²

ⁿⁿ i=1 i =1

₁ [( n_ 1) r' ] [( n_ 1) r' ]

= — £ sn(Xi/n) -Vn £ (Xi+1 /n - Xi/n)²,

n i=1 i=1

with Sn(X_i/_n) = 0 and (X_i+₁ /,_n - X_i/_n)² = 0 for i > L(n - 1)rJ, the result then follows by
the continuous mapping theorem.