Testing for One-Factor Models versus Stochastic Volatility Models

(i)c The statistic Z_n,_m,_r can be rewritten as

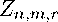
√— L (ⁿ-¹) ^rJ

— £ (S²_n(Х_г/_п) - σ²(Х_г/_п))

i =1

^s--------------------------------S/--------------------------------'

An,m,r

—

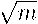
L ( m— 1) rJ

j=1

'm ^{- X}j/m) ^{- σ σ}²⁽^Xs^)dS
JO

Bm,r

√— ^l⁽ⁿ^-¹)^r^J r

+— ∑ σ²(Xi/n) - V— I σ²(Xs)ds.

ⁿ i=1 ^0o

'-----------------------------------_v-----------------------------------'

C n,m,r

(23)

Note that A_n,_m,_r = op(1) by Lemma 2.

We first need to show that C_n,_m,_r = o_a._s.(1). Given Assumption 1(a), Lemma 1, and recalling
the modulus of continuity of a diffusion (see McKean, 1969, pp.95-96),

—— ^l⁽ n- i⁾^r^J

— 52 σ²(Xi/n) -V— σ²(Xs)ds

ⁿ TX -ʃo

^l— ^l⁽ⁿ^-¹)^r^J

— Σ σ ²( Xi/n )
i=1

^l⁽ⁿ^-¹)^r^J _r( i+1) /n

— ∑ σ² ( X_s )d s

i=1 ^i/n

(σ²(Xi/n) - σ²(Xs)) ds

^l⁽ⁿ^-¹)^r^J _r( i+1) /n

— ∑

i=1 ^i/n

^L⁽ⁿ^-¹)^r^J _r( i +1) /n

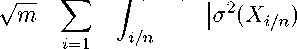
- σ²(Xs)∣ ds

V— sup ∣σ²(X_s) - σ²(X_τ)∣ ≤ V— sup ∣Vσ²(X_τ)∣ sup ∣X_s - X_τ∣

|s—τ ∣≤ 1 /n τ ∈ [0 ,r ] |s—τ ∣≤ 1 /n

s∈ [θ ,r ] s∈ [θ ,r ]

V—iC>₍₁._S( (n^ε/²)Oa.s. (n ¹ /² log n) = 0a.s. (1),

as n¹ /²^ε/²n ¹ /² log n → 0. Thus,

Zn,m,r

Bm,r + ⁰a.s.⁽¹⁾.

The statement then follows from the proof of Step 2 in part i(a).

(i)d The statement follows by the same argument as the one used in part (i)b and by the continuous
mapping theorem.

CorPapers

Testing for One-Factor Models versus Stochastic Volatility Models

More intriguing information