Testing for One-Factor Models versus Stochastic Volatility Models

(ii) We will prove the Theorem for the case analyzed in part (i)c; in the other cases the proof
follows straightforwardly and is therefore omitted. Under H a , we have that

d Xt = μ ( Xt )d t + yptW Wɪ ,_t

^σt = g⁽ ft )

d ft = b ( ft )d t + σ ɪ ( ft )d W₂ ,t.

Pointwise in r, we can rewrite Z_n,_m,_r as

Zn,m,r

,— L ( n-ɪ) rj

m ∑ (Sn(Xi/n) - g (fi/n))

i =1

L ( m— ɪ) rj

^- √^m (^x(j+ɪ)/m ^-^Xj/m)

j=i

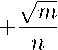
^l⁽^n- 1)^rj

∑ g (fi/n)

i =1

ʌ- ^l⁽^n-ɪ)^rj

m ∑ (Sn(Xi/n) - g (fi/n))

i = 1

'------------------------------->z-------------------------------'

E ʌ-.

n,m,r

([ ( m— ɪ) rj

Σ (^X(j+ɪ)/m ^-^Xj/m)
j=1

I g ( fs )d s

^>Z

√_m L⁽^n- ɪ)^rj r

+— ∑ g (^fi/n) ^- Vm g⁽^fs^)ds.

ⁿ i=1 ^Jo

'----------------------------------------4/-----------------------------------------'

(24)

Ln,m,r

By the same argument used in the proof of part (i)a, Step 4 and Step 2 (respectively) L_n,_m,_r =
o_p (1) and F_m,_r = Op (1).

We can expand E_n,_m,_r as

E ™
n^jn,m,r

^l— ^L⁽^n-ɪ)^rjm

n ⅛

i =1

^ⁿ = 1¹¹ {∖Xj∕n-Xi∕n∖<ξn}ⁿ (^X⁽^j^{+ 1)}^/n^X^j/n) _ ⁽ _f ⁾

I n— ɪ d ^g ∖ⁱ⅛∣El

∖ j=1=1 ¹ {∖Xj∕n-Xi∕n∖<ξn} )

— ^l⁽^n-1)^rjm

n ⅛

i =1

f∑ⁿ n^-ɪ 1flv 2 2n ;2 n f⁽ j⁺¹⁾^/n ( X_s X X₁/_n )√g^(7s)d Wɪ _s ∖

j = ¹ {∖Xj∕n-Xi∕n∖<ξn} j/n ^{s j}∕^{n sj} ɪ^,s

I ^n—ɪ₁ I

∖ ²~=i=i ¹ {∖^χj∕n-Xi∕n∖<ξn}

__Z
>z

^p n,m,r

More intriguing information

1. Evaluating the Impact of Health Programmes
2. The name is absent
3. The name is absent
4. Gender and headship in the twenty-first century
5. Text of a letter
6. The name is absent
7. Evidence of coevolution in multi-objective evolutionary algorithms
8. On the job rotation problem
9. The ultimate determinants of central bank independence
10. The name is absent