Large-N and Large-T Properties of Panel Data Estimators and the Hausman Test

JxT          JxT

Gχ,τA1Gχ,τ + -√t Dχ,τA3Dχ,τ√t^

/ ₁                   J—1

× ( Tθ2^NTGχ,_τA2 ⁺ √t NDDχ,T (A4 ⁺ A5⁾

as (N, T →∞) . Also, by Lemma 2(d), as (N,T →∞) ,

√Nb5 = √N X zizi = op (1).
i

Therefore, the numerator of (94) is

√N (B4 ⁺ B5) ^- C0 μ~7^Al + A3^ μ“TA2 + (A4 + A5)
= √NB4 + Op (1),

as (N,T →∞) . In view of (94), (95) and (96) , we have

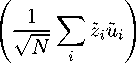
+ op (1) ,

as (N,T →∞) .

Finally, by Lemma 2(c) and Lemma 3, as (N,T →∞) ,

as required. ¥

Part (b)

Under the assumptions in Part (b), as shown for the denominator of (94) ,

as (N,T →∞) . Next, consider the numerator of (94) ,

=(B4+B5)

59

<<   56   57   58   59   60   61   62   >>

More intriguing information