Large-N and Large-T Properties of Panel Data Estimators and the Hausman Test

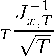
1 1    ∏r≈. J J    J_xT „

√Niπ? ''^ntgx∙^t A^{2 +} √ D

By Lemma 2(d), (b), and (d),

B5 = Op (1),
√NTGχ,τA2 = Op (1),
Dx,T A5 = Op (1) ,

respectively. Under the fixed effect assumption (Assumption 10), Lemma 4
implies that

Dx,T A4 = Op (1) ,

1J          ^-_T¹

_r- ₂ , -XT = o (1) ,
√NtθT Tτ

and

JxT JxT

Gχ,τ AιGχ,τ + -√=-Dχ,τ A3Dχ,τ -√=∙

(as shown in Part (a)), we have

^(B4 + B5) ^- C0 μθ2A1 + A3^   μθ2A2 + (A4 + A5)^ = B4 ⁺ op ⁽¹⁾ .  ⁽⁹⁸⁾

But, according to Lemma 4,

Therefore, (94), (97), (98) and (99) imply
^γg →p ^{γ + (l}Z^ξ1z) ^{1 l}Z^Ξλ,
as (N, T →∞) . ¥

Proof of Theorem 9

Using the notation in (87), we can express the Hausman test statistic by

[(A1 + θTF1¢ ¹ √NT (A2 + θTF2) - Af¹√NτA2] 0

× h^σVA1 ^{1 - σ}2 (A1 ^{+ θ2}TF1)  i

× [(A1 + θTF1)^-1 √NT (A2 + θTF2) - Af ¹√NτA2] .

60

<<   57   58   59   60   61   62   63   >>

More intriguing information