Network
y j= [1...m ]
x i= [1...n ]
Optical Flow Network
line process
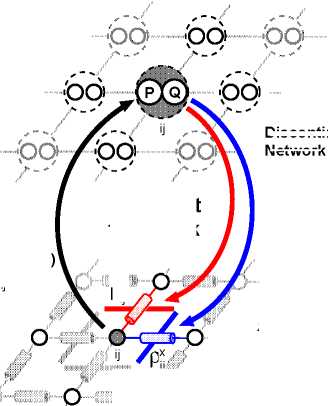
Fig. 2. System architecture.
recurrent
feedback
Discontinuity
Vij=(ui,,Vj)
Fij
ρy
ij
array, nearest-neighbor connections in between units were
dynamically set according to the local optical flow gradi-
ents.
In the following, we present a novel 2D focal-plane pro-
cessor that provides enhanced optical flow estimates using
dynamically controlled connections between its computa-
tional units.
2. COMPUTATIONAL ARCHITECTURE
The computational architecture of the processor is schemat-
ically illustrated in Figure 2. It consists of the optical flow
network and the discontinuity network that are recurrently
connected.
The optical flow network is the physical embodiment
of a dynamical system that, in steady state, solves the con-
straint optimization problem of minimizing the cost func-
tion
Hqf ь ⅞ + pijSij + bias term). (1)
и
Thi cot function epreents the model of visual motion the
systems applies and is described by three constraints im-
posed on the expected and allowed optical flow fields: It
requires the optical flow at each location (i,j) to obey the
brightness constraint2 (Fy), to be smooth (Sŋ) and biased.
Applying gradient descent on the cost function directly pro-
poses the necessary network dynamics in order to solve the
problem. Thereby, the components of the optical flow vec-
tors uij, υij are represented by the analog states of the units
in the network. The network closely follows previous ap-
proaches of solving optimization problems in networks [6],
2thus applying a gradient-based optical flow approach
although its units have a linear activation function and con-
nectivity is restricted to nearest neighbors. Further details
on the network architecture and an extended analysis can be
found in [1, 7].
In the context of this paper, there are two important
points to consider: i) the weight of the smoothness con-
straint in the overall optical flow model is determined by
the conductance pattern that effectively determines the
connectivity strength of the local nearest-neighbor connec-
tions; ii) the network is proven to be globally asymptotically
stable for any given, positive distribution . As a conse-
quence, we can preserve discontinuities in the optical flow
estimate if we find a possibility to control the smoothness
conductances locally at motion boundaries; and still, the
network remains asymptotically stable.
The additional discontinuity network provides this pos-
sibility where the states of its units Fy and Qij (see Fig-
ure 2) recurrently control the lateral conductance p? and
of the optical flow network in the x- and y-direction re-
spectively. For simplicity we refer in the following only to
one type of units (F). We assume the discontinuity units to
have a very narrow sigmoidal activation function д : pij →
Pm ∈ [0,1], meaning that a motion discontinuity at node
ij is, basically, either detected (Pij = 1) or not (Pij = 0).
Thus we rewrite the local conductances in the x-dir≡ction as
p⅞=Po(l-F⅛). (2)
The task, and thus the behavior of the discontinuity net-
work is defined again as optimization problem with the fol-
lowing constraints: i) the total network activity should be
low in order not to split the visual scene into too many in-
dependent motion sources and ii) activity should be high
preferably at locations where the optical flow gradient (∆v)
is large and the brightness constraint is severely violated
(ΔF). As we will see later, the violation of the brightness
constraint serves as an inevitable error measure to achieve
a piece-wise smooth optical flow estimate and thus perform
motion segmentation. The constraints are combined to form
the cost function
Hp = ∑y((ι - ⅞)H(Mdl + 7∣l(∆nj]
+"⅞ + ⅜βp-1(eM) (3)
where , and are weighting parameters and is some
symmetric measure. The integral term represents the total
activation energy needed to keep the unit’s activation state
high or low. Gradient descent on (3) then leads to the fol-
lowing dynamics
⅜ = -⅛(¾ + « - [^ll(∆^)b'll +7∣I(δf⅛∣∣]). (4)
C ∏
We recognize that the units in the network perform a thresh-
old operation, which approximates in steady state a binary
II - 333