Target Acquisition in Multiscale Electronic Worlds

14

Figure 12. Space-scale representation of the fish-eye visualization technique with navigation operations.
Left: spherical; right: linear.

Since the view contains representations of different parts of the document at different scales,
its representation in a space-scale diagram is no longer a horizontal line segment (Figure 12).
Reaching targets with a fish-eye view involves both panning the view and moving the focus
point of the distorted area. As shown by Gutwin (2002), the latter hinders performance
because objects move as they are focus-approached. Some prototypes, however, fix the focus
point at the center of the view, so the user can pan only the view.

3.3.3. The Pan-and-Zoom Technique

Pan-and-zoom uses a single view which shows the document at a uniform scale (Perlin and
Fox, 1993). Panning is used to move the view at a fixed level of scale, while zooming is used
to change the current scale of the view. Zooming occurs around a focus point which is left
invariant by the scale change. The focus point is generally coincident with the center of the
view, more rarely with the cursor position. In a space-scale diagram, zooming amounts to
moving the view along the great ray that goes through the focus point (Figure 13).

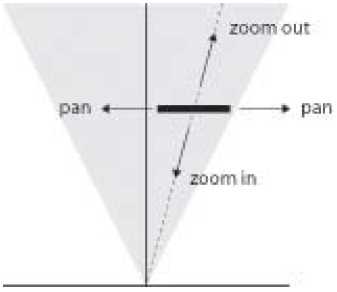
Figure 13. Space-scale representation of the pan-and-zoom visualization technique with navigation
operations.

Zooming appears continuous on the screen, but is actually achieved by multiplying the current
scale by a fixed zoom factor, f, when zooming-in, or, inversely, dividing by f when zooming-
out. The scale values that are navigated by zooming thus follow a geometric, rather than
arithmetic, series, i.e. a power law.

In order to measure distances on the scale dimension, we introduce the zoom index, z = log s,
where s is the scale. Navigating the scale dimension increases or decreases the zoom index by
a constant factor zf = log f :

zoom-in: z' = log s' = log s.f = log s + log f = z + zf
zoom-out: z' = log s' = log s/f = log s - log f = z - zf

We normalize the zoom-index dimension by using the logarithm in base f and therefore zf = 1.
Controlling the zoom index rather than the scale is the key to efficiently navigating a large
range of scales. Typically, a zoom factor of 1.1 allows continuous zooming. With this zoom
factor, the zoom-index range [-50, 50] corresponds to a scale range of approximately [1/100,
100], i.e. a ratio of 10,000 between the smallest and largest scale, while the zoom-index range
[-100, 100] corresponds to a scale range of approximately [1/15,000, 15,000], that is, a ratio
of 225 million.

<<   11   12   13   14   15   16   17   >>

More intriguing information