Target Acquisition in Multiscale Electronic Worlds

17

zoom-index space, which is the only space where distances in scale can be computed, the
zoom-index distance (ZD) is log sout - log sin.

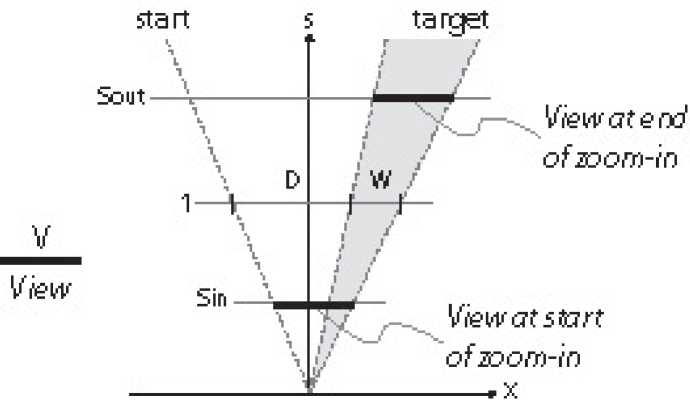
Figure 16. Multi-scale pointing towards a target. D and W are measured at scale 1. S_in and S_out correspond
to the start and end of the zoom-in phase.

ZD is computed using the scaling invariant (equation 3). We first compute sin and sout. At
scale sin, the view (size V) covers the distance D to the target, and the target itself (size W), so
we have:

(D + W) / 1 = V / sin or: sin = V / (D + W)

At scale sout, the view (size V) covers the target (size W) so we have:

W / 1 = V / sout       or: sout = V / W

We now compute ZD:

ZD = log sout - log sin = log V/W - log V/(D+W) = log (D+W)/W = log (1 + D/W) = ID
Therefore the distance to navigate in zoom-index space is exactly the index of difficulty (ID)
of the task. Note that this is independent of view size V: indeed, a smaller view would require
starting at a lower scale, but the task would be completed at a lower scale as well.

4.2. From the Steering law to Fitts’ law

The view pointing task described above is reminiscent of a steering task (Accot & Zhai,
1997): from the moment the target is in the view, zooming-in is similar to driving a vehicle
through a tunnel. The driver uses the accelerator to proceed through the tunnel and turns the
wheel to correct any current aiming error. Here, the user zooms-in toward the target and pans
to correct any aiming error. If the target moves out of view (the user is off the road), the user
must zoom-out (back up) until the target gets back into view and then zoom-in again. For
successful navigation, the target must stay within the view while zooming-in proceeds, just as
the car must stay inside the tunnel while traversing it. Therefore we can use Accot and Zhai’s
(1997) steering law for tunnels to predict navigation time:

MT = k d / w

where d is the length of the tunnel and w its width. In our case, d is the distance navigated
along the scale dimension, which we have shown to be equal to the index of difficulty ID, and
w is the target size of the view, which we call V. Therefore we have:

MT = (k / V) ID                                            (4)

<<   14   15   16   17   18   19   20   >>

More intriguing information