117
Q Zs
(4.20)
Thus the discretized strong-weak system is
∂t
Vw
Cγ∏^s
0
0
N(vs(t),ws(t))
ɪ ∣^B‰(t)
2πα∆τ Is(t)
(4.21)
which is of the same form as (4.14). The notable exception here is that the inputs
are now given according to their local indices.
Model reduction of this system follows in the same manner as that of §4.1.1-4.1.2,
yielding the reduced strong-weak system for arbitrary morphologies:
∂t
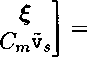
. U7’ ((⅛‰,3)C)
U7HsU
CmVs
0
RN(U(:, z)v3, ws)
0
UτΦ
ɪ ∣^B‰(t)^
2πa∆x [uτIs(t) '
(4.22)
One important point should be made concerning the selection of snapshots for
both the POD and DEIM. Although it may seem reasonable to take snapshots of
the strong branches from the simulation of the strong-weak system, this yielded very
poor results for realistic morphologies. However, if the snapshots are taken of these
branches from the full system simulation then the results improve dramatically.
More intriguing information
1. The name is absent2. CAPACITAÇÃO GERENCIAL DE AGRICULTORES FAMILIARES: UMA PROPOSTA METODOLÓGICA DE EXTENSÃO RURAL
3. The name is absent
4. Markets for Influence
5. How Offshoring Can Affect the Industries’ Skill Composition
6. The name is absent
7. Does Market Concentration Promote or Reduce New Product Introductions? Evidence from US Food Industry
8. The name is absent
9. Short report "About a rare cause of primary hyperparathyroidism"
10. The Role of Immigration in Sustaining the Social Security System: A Political Economy Approach