Performance - Complexity Comparison of Receivers for a LTE MIMO–OFDM System

KETONEN et al. : PERFORMANCE-COMPLEXITY COMPARISON OF RECEIVERS FOR A LTE MIMO-OFDM SYSTEM

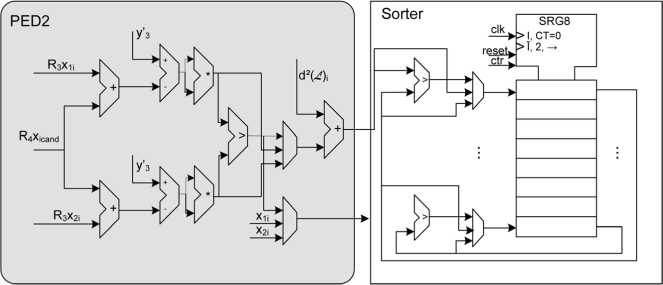
Fig. 12. Parallel PED calculation and sorting.

TABLE IV

The 2 × 2 K -Best LSD Receiver Complexity

and the final K symbol vectors are demapped to bit vectors and
their Euclidean distance is used in the LLR calculation.

The modified ∕√-hcst LSD tree search was used in the imple-
mentation in the 64-QAM case. The architecture of the second
stage parallel Euclidean distance calculation and insertion
sorting is illustrated in Fig. 12. Two PEDs are calculated in
parallel and the smallest one is added to the list.

The 2 x 2 ∕√-hest LSD receiver complexity is shown in
Table IV and the 4×4 receiver complexity in Table V. Seven
BRAMs are needed to store the results of the QRD in a 5-MHz
bandwidth. In the iterative 2× 2 64-QAM 16-best LSD, addi-
tional 9 BRAMs are needed to store the list and LLRs from
the previous iteration. The clock frequency in the ASIC imple-
mentation is 140 MHz and in the FPGA implementation from
100 MHz to 94 MHz depending on the modulation.

The word lengths for the λ-best LSD and LLR calculation
are mainly 16 bits and computer simulations have been per-
formed to confirm that there is no performance degradation [24].
The sorters are insertion sorters. The list size values of 16 and
8 are used in the implementation. The sorters have 16 or 8 reg-
isters in which the smallest Euclidean distances are kept during
the sorting depending on the list size. A full list is used in the
QPSK case and no sorting is required. This decreases the com-
plexity of the detector.

TABLE V

LLR calculation, non-iterative∕iterative

The LLR calculation block was designed both for the iterative
and noniterative receiver. The iterative LLR block was designed
to have a low latency in order to perform additional global it-
erations quickly. The complexity of the block is therefore high.
Using the decoder soft outputs in calculating the LLRs also adds
to the complexity. If extra iterations are not needed, the LLR
block can be scheduled to have the same latency as the ∕∖-best
LSD and have a lower complexity.

B. Soft Interference Cancellation

The SIC receiver consists of a LMMSE detector, a LLR cal-
culation block, a symbol expectation calculation block and an
interference cancellation block as presented in Fig. 4. The top
level architecture of the LMMSE detector for a 2 × 2 antenna
system is presented in Fig. 13. The channel matrix H is first mul-
tiplied by its complex conjugate transpose and the noise vari-
ance σ² is added to the diagonal elements. The resulting 2 × 2
matrix G is positive definite and symmetric. This simplifies the
matrix inversion, which is performed by dividing the elements
with the determinant, switching the diagonals and negating the
off-diagonal elements. The determinant is real valued and the
off-diagonal elements are complex conjugates. Therefore, less
operations are needed.

The architecture for the real part of the symbol expectation
calculation in the 16-QAM case is presented in Fig. 14. The
imaginary part is calculated in parallel in the same manner from

<<   <   5   6   7   8   9   10   11   >   >>