Geography, Health, and Demo-Economic Development

gets large because of the declining impact of average income on fundamental child survival. At
middle stages of development, however, the second term increases because of improving funda-
mental rates of child survival, i.e. decreasing (1—π). Thus, we observe a hump-shaped correlation
between population growth and income. At the lowest stages of development the subsistence
effect dominates and population growth is positively correlated with per capita income. First,
when income rises from subsistence level parents want to have larger families. This effect, how-
ever, vanishes quickly and the quantity-quality substitution effect becomes dominating. When
more children survive and income is well above subsistence level, parents want to spend more
on each child and prefer a smaller family.

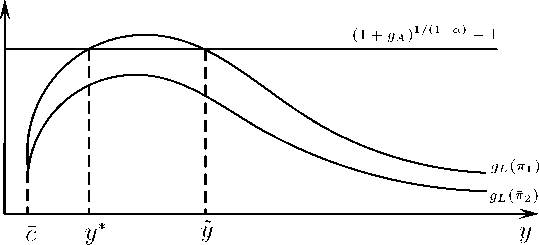
Figure 3: Patterns of Population Growth

At the same time, however, the partial effect of fundamental child survival on population
growth is negative for any given income level, i.e. using (6c) and (7a)

∂gL  ∂n       ∂π      nπ                     ∂h      nπ

-⅛L = . ∙ ∏ + n ∙7F = ~t_λ---T + n ¹ — λh + (1 — ∏ λ = —---≡ < 0.    (11)

∂π ∂π        ∂π (1 — π)π    ∖                ∂π /     1 — π

Consider two regions 1 and 2 with π₁(y) < π₂(y) implying that for any given income population
grows at a higher rate in the unfavorable location 1. Irrespective of whether the demo-economic
system is in its first phase of positive correlation between income and population growth or in its
second phase of negative correlation, parents in the unfavorable region always have a comparative
advantage in fertility. In other words, at high fundamental survival rates child expenditure
consists to a lesser degree of β3-components motivated by child survival (i.e. nutrition and
health expenditure) and to a higher degree of β4-components motivated by child quality (i.e.
schooling). Thus, the Beckerian child-quality trade-off is stronger; child expenditure substitutes

11

<<   10   11   12   13   14   15   16   >>

More intriguing information