Spectral calibration of exponential Lévy Models [1]

Denis Belomestny and Markus Reiβ

Making use of R₀U 2ue^cu2 du =    —¹ = E (cU2) U² for any c > 0, we esti-

mate the last integral by

U2

e eT^σr^u +2TЫь 1 ∣u∣^s+2 du 6 e2T^kμkL¹ U^s+3E(T'.U2)

—U

and derive from ∣∣μ∣∣^ 1 = Fμ(0) 6 2R for the bias part in the linear term

∣L>∣ . ∆2E(T2U2).

For the variance part of the linear error term we use the support proper-
ties supp(w_σ^U) ∈ [-U, U] and supp(bk) = [xk—1, xk+1]. Several applications
of the Plancherel identity, the Cauchy-Schwarz inequality and estimate (35)
then yield

2

— i)^—1(u — i)uF b_k (u)w_σ^U (u) du^I

Altogether we obtain for the linear error term

E

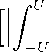
2

L(u)wσ(u)du∣ ] . E(Tσ2U2) (∆⁴ + U^-1 ∆∣∣δ∣∣2^).

It remains to estimate the quadratic remainder term. Due to Lemma 1
and Proposition 2 we have

E

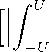
2

R(u)w_σ^U (u) duI^I

(40)

^{U U I                            I2} u⁴w^U (u)v⁴w^U (v)

< E E F ( O-O )( u ) F ( O-O )( v )∣ ---^σ. ( ) , ^σ2 ( ) d u d v.

_{-U -U}                                       κ(u)²κ(v)²

The independence of (εk ) and the finiteness of their fourth order moments
entail the inequality

<<   16   17   18   19   20   21   22   >>

More intriguing information