Graphical Data Representation in Bankruptcy Analysis

W. K. Hardle, R. A. Moro, and D. Schafer

Accuracy Ratio

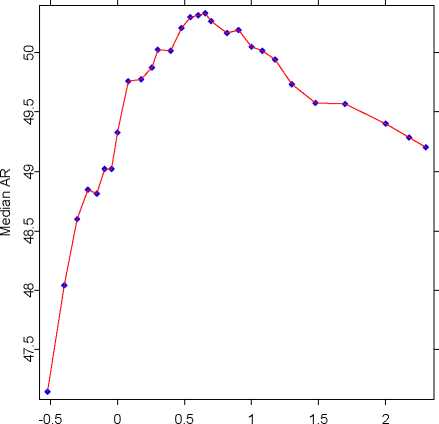
log10(r)

Fig. 7. The relationship between an accuracy measure (AR) and the coefficient r
in the SVM formulation. Higher r’s correspond to less complex models. The median
ARs were estimated on 100 bootstrapped subsamples of 500 solvent and 500 insol-
vent companies both in the training and validation sets. A bivariate SVM with the
variables K5 and K29 was used. We will be using r = 4 in all SVMs used in this
chapter.

We have also conducted experiments with subsamples of the size of 5000
observations. The change of median was extremely small (one-two orders of
magnitude smaller than the interquartile range). The interquartile range got
narrower as it was expected, i.e. the difference between models with bigger
samples is only more statistically significant. Thus, proving that if the differ-
ence is significant on a sample of 1000 observations, it can be guaranteed that
this will remain so for bigger samples.

The SVM based on variables K5, K29, K7, K33, K18, K21, K24, K33 and
K9 attains the highest median AR of around 60.0%. For comparison we plot
an improvement in AR for the SVM vs. DA and logit regression on the same
100 subsamples. The data used in the DA and logit models were processed
as following: if xi < q0.05 (xi) then xi = q0.05 (x) and if xi > q0.95 (xi) then
xi = q0.95(xi); i = 1, 2, . . . , 8; qα(xi) is an α quantile of xi. Thus, the DA and
logit regression applied were robust versions not sensitive to outliers. Without
such a procedure the improvement would be much higher.

<<   8   9   10   11   12   13   14   >>

More intriguing information