Graphical Data Representation in Bankruptcy Analysis

W. K. Hardle, R. A. Moro, and D. Schafer

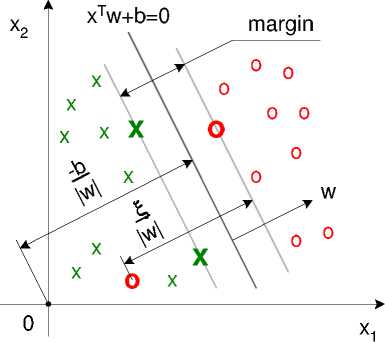
Fig. 4. The separating hyperplane x^τw + b = 0 and the margin in a non-separable
case. The observations marked with bold crosses and zeros are support vectors. The
hyperplanes bounding the margin zone equidistant from the separating hyperplane
are represented as x^τw + b = 1 and x^τw + b = -1.

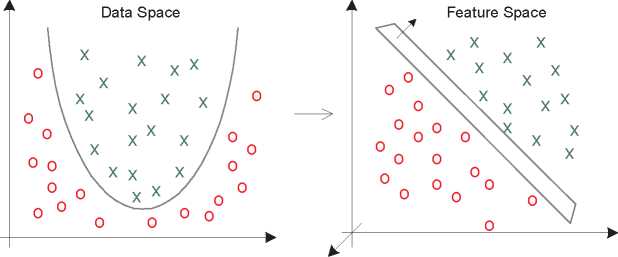
Fig. 5. Mapping from a two-dimensional data space into a three-dimensional space
of features R² → R³ using a quadratic kernel function K(xi, xj) = (x_i^τxj)². The
three features correspond to the three components of a quadratic form: x₁ = x21, x₂ =
√2x₁x₂ and X3 = x2, thus, the transformation is Ψ(x₁, x₂) = (x², v^z2x₁x2, x2)^τ. The
data separable in the data space with a quadratic function will be separable in the
feature space with a linear function. A non-linear SVM in the data space is equivalent
to a linear SVM in the feature space. The number of features will grow fast with d
and the degree of the polynomial kernel p, which equals 2 in our example, making
the closed-form representation of Ψ such as here practically impossible