Testing the Information Matrix Equality with Robust Estimators

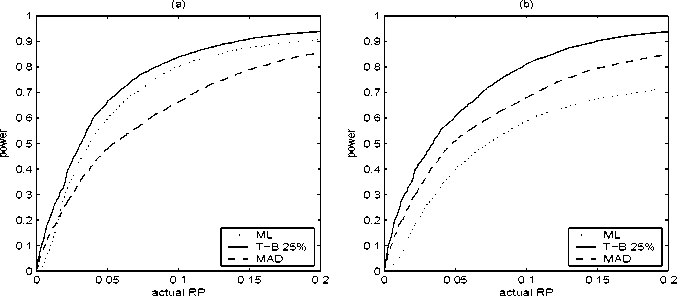
Figure 7: RP-Power curves: (a) n = 20, 2 outliers at 4 (b) n =20,
one outlier at -4, one outlier at 4

correct power for errors in rejection probability (ERP) ² we plot power as
function of (actual) rejection probability under the null of correct specifi-
cation, as in Davidson and MacKinnon (1998). For pivotal statistics, such
an RP-power curve ³ is obtained as follows. Run R Monte Carlo replica-
tions under the null and under the alternative hypothesis. Order the R test
statistics obtained under the null from high to low to obtain T₁⁰ ≥ ... ≥ T_R⁰ .
The power at actual RP k/(R + 1) is then estimated as the fraction of test
statistics generated under the alternative that are larger than T_k⁰ . Figure 7
plots the RP-power curves for n = 20, the alternative hypothesis being the
normal distribution contaminated with (a) two outliers at 4 and (b) one
outlier at -4andoneat4. From Figure 7 (a) it is clear that the IM test
with robust estimators may, but need not be, more powerful in the presence
of outliers than the IM test with ML estimator. As a second alternative hy-
pothesis we consider the Cauchy distribution. The RP-power curves for the
Cauchy distribution are plotted in Figure 8. As conjectured, the IM tests
with robust estimators have more power. A χ₃² alternative is considered in

²The ERP of a test is the actual minus the nominal (i.e. chosen) probability of rejecting
the null when it is true.

³ Davidson and MacKinnon (1998) call this a size-power curve. Because the size of a
test, defined as the supremum, over the null, of the RP, often differs from the RP, we
prefer the term RP-power curve. In this particular model, however, the statistic is pivotal
and hence size equals RP.

21

<<   20   21   22   23   24   25   26   >>

More intriguing information