Testing the Information Matrix Equality with Robust Estimators

(a) Power surface ML estimator; (b) difference ML

estimator-other

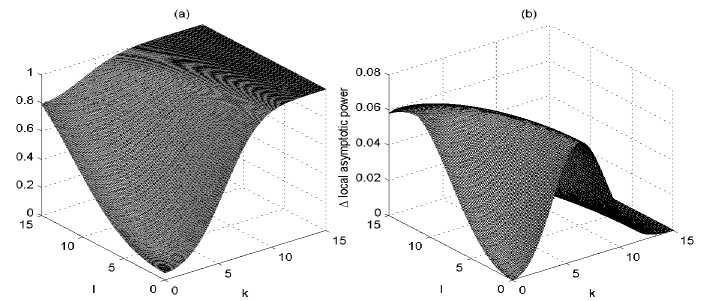
The power surface for the IM test with ML estimator is plotted in Fig-
ure 6 (a). The difference in power between the IM test with ML estimator
and the IM test with other M-estimators is plotted in Figure 6 (b). The
maximal difference in power is 0.06623. It is again observed that the loss in
local power when using robust estimators for the IM equality test is rather
limited.

5 The normal regression model

For the normal model with covariates, Fθ(y∣x) = σΦ(^y X ^β) with θ =
(β',σ)'. We obtain, with u = (Y — X'β)/σ,

1    ( u² — 1)vech( XX^, )

m (X, Y ; θ) = 2       (u³ — 3u) X

^σ      u⁴ — 5u² +2

where vech(■ ) is the lower triangular stack operator, and ξ = ξ(X, Y; θ),

₁ / ( u² — 1)vech( XX ' ) — σ IF( X, Y ; ^; K, F_θ ) Ek [vech( XX ' )]

ξ = 2                         ( u³ — 3 u ) X

^σ              u⁴ — 5u² + 2 — σIF(X,Y; ^; K,F_θ)

18

<<   17   18   19   20   21   22   23   >>

More intriguing information