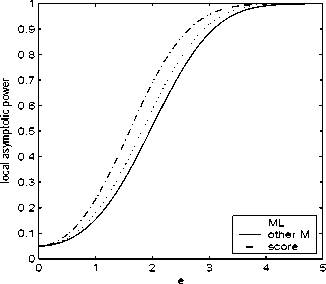
Figure 4: Power curves: Student’s t
Let S be the score test statistic, defined in the usual way. Under the
null hypothesis (p = ∞), S has a limiting χ2 distribution. Under Hn, as we
show in Appendix C.1,
S →d χ12(δ),
with non-centrality parameter
In conclusion, the score test and the IM tests have the same non-centrality
parameter in their limiting distribution. The power curves (as a function
of e) of 5%-level tests are given in Figure 4. The differences in power are
entirely due to differences in degrees of freedom: 1 for the score test, 2 for
the IM test with the ML estimator, and 3 for the IM test using any other
M-estimator. The difference in power between the IM tests is small.
4.3 Skewed normal alternative
Let Z — N(0, 1) and denote the distribution of ZI(Z ≤ 0) + (1 + γ) ZI(Z >
0) as FYk (Fernandez and Steel, 1998). Under the sequence of local alterna-
tives
Hn : Y
- Fn = Fesk√n,
15
More intriguing information
1. Keystone sector methodology:network analysis comparative study2. Second Order Filter Distribution Approximations for Financial Time Series with Extreme Outlier
3. The name is absent
4. The name is absent
5. fMRI Investigation of Cortical and Subcortical Networks in the Learning of Abstract and Effector-Specific Representations of Motor Sequences
6. The name is absent
7. National urban policy responses in the European Union: Towards a European urban policy?
8. The demand for urban transport: An application of discrete choice model for Cadiz
9. Sex-gender-sexuality: how sex, gender, and sexuality constellations are constituted in secondary schools
10. Dual Inflation Under the Currency Board: The Challenges of Bulgarian EU Accession