From (17) we get:
∂h
∂E = 1
E τ⅛
δ
1 β (1 - δ) = E ⅛β
1 + β - 2βδ 1 + β -
and also:
∂h
∂β
„1 (1 - δ) (1 + β - 2βδ) - β (1 - δ) (1 - 2δ)
E 1—0
(1 + β - 2βδ)2
■ 1 + β — 2βδ — δ — βδ + 2βδ7 — β + 2βδ + βδ — 2βδ7
Ej 1 — δ --------------------------------------------------------------------------------------------
(1 + β — 2 ••■■■ 2
ι 1 — δ
E I—0 -----------------
(1+ β — 2βδ)2
and then:
∂h
∂δ
1 — β (1 + β — 2βδ) + 2β2 (1 — δ)
Ej 1—0 -------------------------------------------------------
(1 + β — 2βδ)2
β(1 — δ) 1 1
1 + β — 2βδE—S (1 — δ)2
log E =
E —β — β2 + 2β2δ + 2β2 — 2β2δ + Eʌ β l σ E
(1 + β — 2βδ)2 + (1 — δ)(1 + β — 2βδ)lθg
1
E1-0
β2 — β
(1+ β — 2βδ)2
1
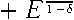
β
(1 — δ)(1 + β — 2βδ)
log E =
E 1⅛ ∣^ β (β — 1) , β
1 + β — 2βδ [1 + β — 2βδ + 1 — δ
From (18) we have:
∂ρ = (α (ξ + η + θ) — ξ) η — αη (ξ + η + θ) =
dα ^ (α (ξ + η + θ) — ξ)2 ^
αξη + αη2 + αθη — ξη — αξη — αη2 — αθη ξη
(a (ξ + η + θ) — ξ)2 (a (ξ + η + θ) — ξ)2
and then:
∂ρ -№п ∙ α α2η
dθ (α (ξ + η + θ) — ξ)2 (α (ξ + η + θ) — ξ)2
and also:
∂ρ —oq (α — 1) αη (1 — α)
dξ (a (ξ + η + θ) — ξ)2 (a (ξ + η + θ) — ξ)2
and finally:
∂ρ (α (ξ + η + θ) — ξ) α — αη ∙ α
dη ~ (α (ξ + η + θ) — ξ)2 "^
α2ξ + α2η + α2θ — αξ — α2η α [α (ξ + θ) — ξ]
(a (ξ + η + θ) — ξ)2 (a (ξ + η + θ) — ξ)2
33
More intriguing information
1. Centre for Longitudinal Studies2. Factores de alteração da composição da Despesa Pública: o caso norte-americano
3. Financial Development and Sectoral Output Growth in 19th Century Germany
4. The name is absent
5. The name is absent
6. The name is absent
7. The Response of Ethiopian Grain Markets to Liberalization
8. Knowledge, Innovation and Agglomeration - regionalized multiple indicators and evidence from Brazil
9. Social Balance Theory
10. The name is absent