Similarly player 2 prefers agenda 1 when λ is sufficiently large (at the limit λ>λRe
with λRe = αα1(++α-) 1 ), otherwise, he prefers agenda 2. Since in this case λ cannot be
larger than λGR , then both players prefer agenda 2 if 0<λ<min {λY e, λRe, λGR}
(see fig. 1) otherwise players have different preferences over agendas.
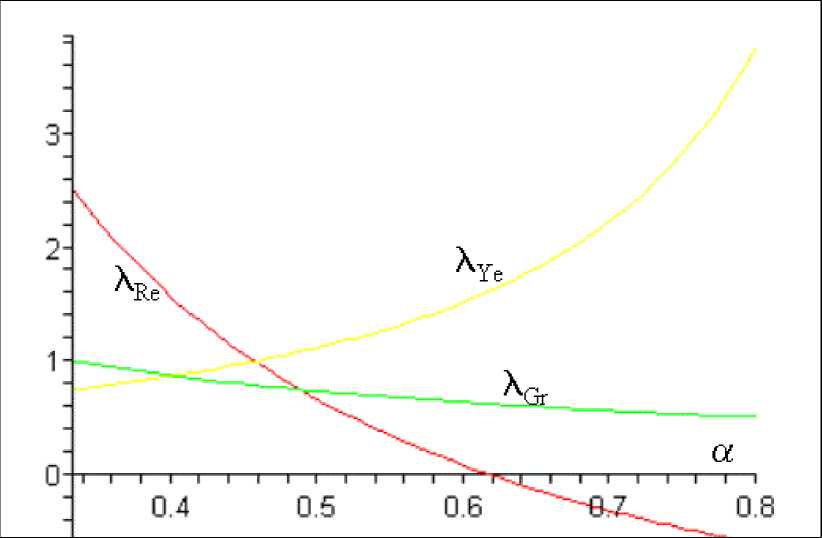
Agreement arises only for 0 <λ<min {λYe,λRe,λGR}
B) Let λB < λ < 1, with λB = VEII+")—α, then Player 1 demands x1 as in (55)
while in Agenda 2 player 1 obtains the entire surplus. Player 1 prefers agenda 1 if
λ > λG with λG = -(1 — a) + 2+ + a2 and agenda 2 otherwise, while Player 2 always
prefers agenda 1 unless α<0.5 and λ is in [λY , 1] with λY
(1—a)-√ 1 —2α
α
. Then,
31