for λB <λ< 1 and α> 0.5 players never agree over agenda, while for α< 0.5 and
max {λB ,λY } <λ<λG (see fig. 2) both players prefer agenda 2.
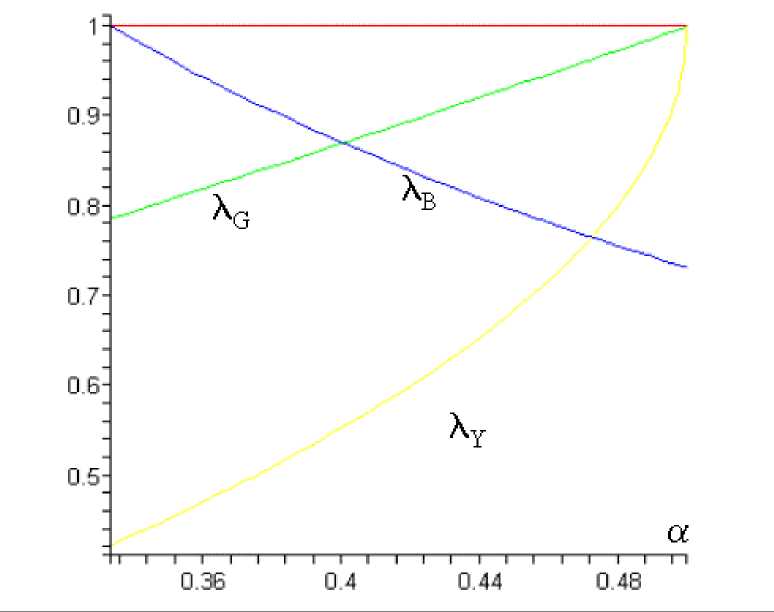
Agreement arises for max{λB,λY } <λ<λG
C) Let 1 < λ < α + ʌ/a(l + α), then in agenda 1 player 1 demands x1 as for case
B), while in agenda 2 in equilibrium player 1 obtains ag2 xe1 as defined in (60). In this
case, since λ> 1, it is straightforward to show that player 1 always prefers agenda 1
while player 2 always prefers agenda 2.
D) Let λ>α+ α(1 + α), then player obtains the entire surplus in agenda 1 and
32
More intriguing information
1. Income Taxation when Markets are Incomplete2. Constructing the Phylomemetic Tree Case of Study: Indonesian Tradition-Inspired Buildings
3. Research Design, as Independent of Methods
4. The name is absent
5. A Duality Approach to Testing the Economic Behaviour of Dairy-Marketing Co-operatives: The Case of Ireland
6. Short- and long-term experience in pulmonary vein segmental ostial ablation for paroxysmal atrial fibrillation*
7. DIVERSITY OF RURAL PLACES - TEXAS
8. Altruism and fairness in a public pension system
9. Rent Dissipation in Chartered Recreational Fishing: Inside the Black Box
10. Short report "About a rare cause of primary hyperparathyroidism"