12
ce qui conduit a
Pour z > zc
TMz = TMc + 1/Vmax * [Dz -≡Vmax2 / amax)]. (7)
Si Ac ne peut pas etre estimё selon le critere de Γemergence du plateau de vitesse, l'Equation
7 peut remplacer l’Equation 4. Dans tous les cas, il apparait clairement que, pour un ID
constant, lorsque la valeur critique d’echelle est dёpassёe, le TM commence a dёpendre du
facteur d’echelle par l'intermёdiaire de Dz : l'invariance d'eclιelle de la loi de Fitts est brisёe.
2.2.7. Optimisation de Tamplitude pour les mouvements a grande echelle
Dans l’intervalle d’isochronie, jusqu’au niveau z c, on peut prevoir que l’amplitude couverte
sera en moyenne approximativement ёgale a la distance de la cible, c’est a dire que A ≈ D, le
sujet ayant intёrёt a viser le milieu de la cible pour minimiser le risque d’erreur. Toutefois,
une telle strategic n’est plus optimale a grande echelle : il devient efficace de pointer en-deςa
du centre de la cible (A < D) sans risquer d’accroitre le taux d’erreur.
L’optimum de Az pour tout z > zc se calcule aisement. Si le sujet continue d’appliquer a
grande echelle les consignes de la tache de Fitts, alors les conditions cinematiques de la
deceleration seront invariables et identiques a celles qui prevalaient au niveau d'echelle
critique : le freinage va commencer a partir de la meme vitesse de croisiёre, egale a Vmax, et le
processus de deceleration se deroule identiquement pour tout z > zc. La strategie optimale
consiste donc a pointer a une distance constante au dela du bord proximal de la cible. Cette
distance correspond a la demi-largeur de la cible a l'echelle critique, soit ½ Wc (Figure 11).
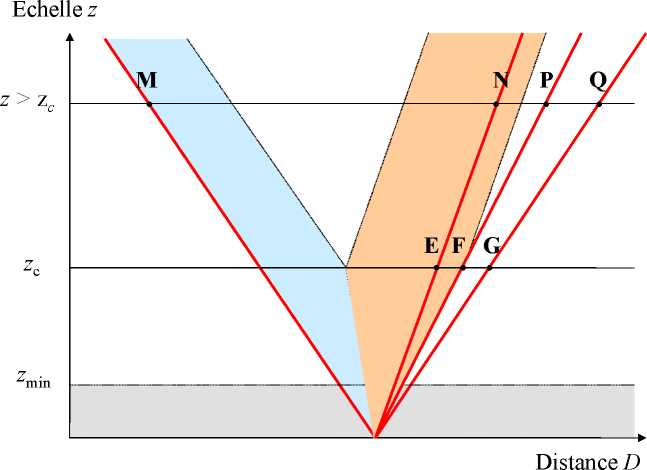
Figure 11. Calcul de l’optimum theorique d’amplitude dans le pointage a grande echelle. Pour tout z > zc, le
freinage doit se terminer juste au-dela du bord proximal de la cible, la distance de depassement correspondant au
segment EF, egal a ½ Wc.
On en deduit ainsi que, pour z > zc,
A z = D z — ½ Wz + ½ Wc
Ce qui, une fois adapte au protocole reciproque, devient
More intriguing information
1. The WTO and the Cartagena Protocol: International Policy Coordination or Conflict?2. CONSIDERATIONS CONCERNING THE ROLE OF ACCOUNTING AS INFORMATIONAL SYSTEM AND ASSISTANCE OF DECISION
3. Secondary stress in Brazilian Portuguese: the interplay between production and perception studies
4. The constitution and evolution of the stars
5. Philosophical Perspectives on Trustworthiness and Open-mindedness as Professional Virtues for the Practice of Nursing: Implications for he Moral Education of Nurses
6. Nach der Einführung von Arbeitslosengeld II: deutlich mehr Verlierer als Gewinner unter den Hilfeempfängern
7. The name is absent
8. The name is absent
9. The name is absent
10. Moi individuel et moi cosmique Dans la pensee de Romain Rolland