17
On pourrait s’imaginer, a partir de notre modёlisation, que la pente de la loi de Fitts
doit tendre asymptotiquement vers zero avec une croissance indefinie de l’echelle puisque le
rapport D/W, en tant que determinant du TM, doit peu a peu s’effacer devant l’amplitude
absolue. La Figure 18 explique pourquoi il ne peut pas en aller ainsi : lorsque la tache est
rescalee au-dela du niveau critique d’echelle, le pourcentage de penetration dans la cible (qui
par construction vaut 50% quand le mouvement s’arrete au centre) se reduit de faςon
monotone, et ce d’autant plus que la cible est plus large et l’ID plus bas. En fait, plus l’echelle
croιt, plus l’amplitude couverte tend a se rapprocher du minimum D - W, la distance separant
les bords internes des deux cibles (Equation 8). Ce n’est pas simplement que la loi de Fitts
devienne fausse au-dela de Zc—plus precisement, le paradigme de Fitts n’est plus applicable.
D’une part, D ne coincide plus avec l’amplitude du mouvement, puisque seule compte, au-
dela du niveau critique d’echelle, la distance au bord interne de la cible ; d’autre part, W ne
coιncide plus avec la tolerance du mouvement, puisque la dispersion du mouvement devient
une constante. L’ID, en d’autres termes, ne rend plus compte des caracteristiques pertinentes
de la tache.
Percent Target Penetration (% of W)
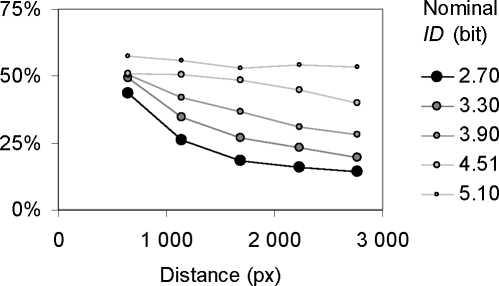
Figure 18. Pourcentage de penetration de la cible en fonction de la distance a couvrir.
Notre modele predit en fait que la pente de la loi de Fitts doit croitre lineairement avec
l’echelle, non pas parce que l’ID est de plus en plus influent, mais pour la raison que l’on
vient juste de donner : plus l’echelle croιt, plus on vise court, mais comme un retrecissement
de la cible contrecarre cet effet, on obtient une influence de l’ID, mais une influence indirecte
et entierement factice. La Figure 17 montre que les points experimentaux, apres s’etre ecartes
de la pente observee au niveau d’echelle le plus bas, rejoignent la prediction du modele.
Tandis que la loi de Fitts, loi d’amplitude relative et donc loi d'invariance d'echelle, est valide
pour les petites echelles, a plus grande echelle une loi d’amplitude absolue prend le relais.
Le fait qu’une loi de relativite d’echelle s’impose peu a peu quand le pointeur doit
couvrir des distances de plus en plus grandes n’a sans doute rien de surprenant. Il nous paraιt
cependant important, dans la perspective d’une meilleure comprehension du paradigme du
pointage, de tenter d’apprehender les deux lois ensemble, et de comprendre la transition de
l’une a l’autre. Nous travaillons actuellement a concevoir une formulation generale de la
relation liant le TM a la geometrie et a l’echelle de la tache dans laquelle la loi de Fitts
apparaιtra comme un cas particulier.