The name is absent

20

difficile (D/W = 109, ID = 30 bits), la tache representait !’equivalent d’un pointage sur des
cibles de 1 cm de diametre situees a 10.000 km l'une de l’autre. Il y a la un elargissement
substantiel du paradigme de Fitts : l’etude classique du pointage, qui interesse depuis
longtemps les sciences cognitives et les neurosciences, s’etend desormais a un contexte inedit,
celui du pointage dans les mondes d’information multi-echelle.

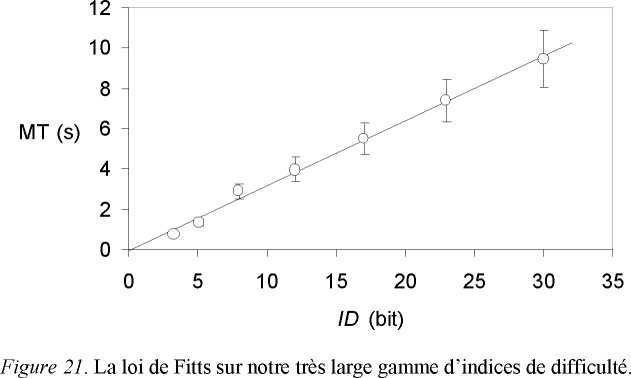
Le resultat principal de l’experience a ete que le temps moyen de pointage etait
proportionnel a l’ID (Figure 21). Il est a noter que la relation illustree, lineaire au sens strict
(c’est a dire sans ordonnee a l’origine), est plus simple que celle que l’on a classiquement
observee dans la gamme etroite d’ID accessible au pointage uni-echelle classique (2-10 bits).
Nous aboutissons ainsi a une generalisation de la loi de Fitts au cas des environnements
d’information multi-echelle, avec une extension considerable de la gamme exploree sur l’axe
de la variable independante.

Les resultats de cette experience sont pleinement compatibles avec Thypothese simple
d’une capacite constante de traitement (ou de transmission) de l’information que Fitts (1954)
avait suggeree a l’origine, en s’inspirant de la theorie de Shannon et Weaver (1949). Dans un
monde multi-echelle, en effet, le pointage manuel devient analogue a la tache consistant a
specifier une carte parmi N cartes au moyen d’une succession de choix hierarchiques. Si le
paquet compte 8, ou 16, ou 32 cartes (c’est-a-dire 2³, 2⁴ ou 2⁵ cartes), la cible sera atteinte
apres 3, 4 ou 5 choix dichotomiques, et des lors le temps necessaire pour identifier la carte
doit varier comme log2N.

<<   17   18   19   20   21   22   23   >>

More intriguing information