Unemployment in an Interdependent World

26 "1

24- .

22-. .

Country 1, ∆ Unemployment

18

16

14

12
1

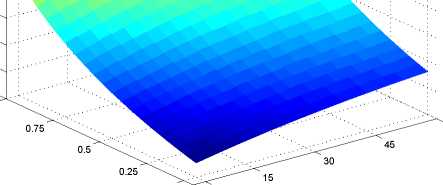
0        0

ν

τ (%)

Figure 5: Change in unemployment [on the vertical axis] as a function of trade costs and
external economies of scale for a given change of b1 from 0.4 to 0.8.

of 0.112.²⁶ Hence, a higher value of γ is associated with less firm heterogeneity; it is,
however, also associated with a lower mean of the productivity distribution. Our main
findings can be summarized as follows:

Result 5 [How firm heterogeneity conditions spill-overs]

The larger the shape parameter of the Pareto distribution describing the distribution of
firm-level productivity, the smaller is the effect on unemployment in all countries triggered
by a given increase in unemployment benefits in country 1.

The more equal firms are concerning their productivity, the less changes in unemploy-
ment benefits affect unemployment in both, the country where the change occurs and the
trading partner country. The effect of unemployment changes shrinks with more equal
firms, as changes in unemployment benefits have only a minor effect on average produc-
tivity. Hence, the competitiveness channel due to lower import competition is weakened,
leading to a smaller reaction of unemployment. For the trading partner, a second fact is
important. If firms are nearly homogeneous, then only few firms are productive enough to
incur the fixed costs for both, the home market and the foreign market. Hence, there is less
trade when firms are more homogeneous. With a γ = 10 and trade costs of τ = 1.6, the
spill-over nearly vanishes, as hardly any firm from country 1 serves the foreign customers.

Note that a value of γ = 10 does not completely shut down heterogeneity. If one
wants to eliminate heterogeneity, the zero-profit cutoff conditions become redundant and
the system of equilibrium conditions essentially collapses to one where the Krugman

²⁶Note that for a Pareto distribution, the variance is given by (_γ-2^γ(^γ_-1)₂ for Y > 2, the standard
deviation is given by -^γr,^γ -‰, and the coefficient of variance is given by , ¹    . Further we assume

γ-1   γ-2                                                       _γ(_γ-2)

that γ > σ - 1 so that the variance of log productivity is finite.

26

<<   25   26   27   28   29   30   31   >>

More intriguing information