Jos muodostetaan uusi muuttuja y = (x-σ2T)/ σ4τ, joka on normaalisti jakaantunut muuttuja
keskiarvolla 0 ja Varianssilla σ2T, voidaan kaava (L2.13) esittââ muodossa
(L2.14) S Prob[y > -log(S∕K) - (r-σ2∕2)T] =
SProbf
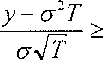
~logGS77Q-(r~σ2∕2)Z
σ√f
VjJ- OiV l-----------ɛ=--------
Sijoittamallayhtalot (L2.12) ja (L2.14) kaavaan (L2.ll) saadaan
(L2.15) C(S1O) = SN[d1 ]- Sexp(-rT)N[d2]1 missâ
dɪ =
d2-~
log(5∕X') + (r + σ2∕2)Z∙
σ√7
ja
∖og(S∕K) + (r~σ2 ∕2)T
σ4τ
Yhtalo (L2.15) on Black-Scholes-hinnoittelumalli eurooppalaiselle osto-optiolle.
Myyntioptio
Myyntioption hinnoittelukaava Voidaanjohtaa edelliseen todistukseen viitaten monella eri
tavalla. Otetaan IahtbtiIanteeksi ajan hetkellâ O muodostettava portfolio, joka muodostuu
riskittômâstâ Sijoituskohteesta, osto-optiosta ja tâmân kohde-etuudesta
(L2.16) Kexp(-rT) - S + C(S1O)
Taman portfolion arvo option erâântymispàivânâ on
(L2.17) K- S(T) + Max [S(T)-K,0] - K-S(T)Jos K ≥ S(T)
OJos K< S(T) => Max [K-S(T)3 0]
More intriguing information
1. The name is absent2. Volunteering and the Strategic Value of Ignorance
3. Searching Threshold Inflation for India
4. Benchmarking Regional Innovation: A Comparison of Bavaria, Northern Ireland and the Republic of Ireland
5. Inflation Targeting and Nonlinear Policy Rules: The Case of Asymmetric Preferences (new title: The Fed's monetary policy rule and U.S. inflation: The case of asymmetric preferences)
6. Trade Openness and Volatility
7. Weather Forecasting for Weather Derivatives
8. Novelty and Reinforcement Learning in the Value System of Developmental Robots
9. Endogenous Heterogeneity in Strategic Models: Symmetry-breaking via Strategic Substitutes and Nonconcavities
10. Behavior-Based Early Language Development on a Humanoid Robot