Kaavassa (L2.11) on kâytetty apuna normaalijakauman tiheysfunktiota ja yhtâiossâ (L2.8)
olleen maksimointifunktion termit on kerrottu diskonttotekijâllâ exp(-rT). Yhtalon (L2,11)
viimeinen rivi voidaan vielà kehittâa Seuraavasti
(L2.12) Sexp(-rT) f —r~ exp(--~)dx -
,i 2 σ∖2πT 2cτ7^
Л. 2
Sexp(-rT) Probfx > -log(S∕K) -(r-σ2∕2)T] =
ς r TAD M x ∣og(S∕∕0 + (r-σ2∕2)7'
Sexp(-rT) Probf--7= <-----------τ=---------]=
σ√ 1 σd l
Sexp(-rT)N[- log(5∕^) + (r~σ3∕2)71 ]
σjτ
Merkinta N[.] viittaa Standardoituun normaalijakauman kertymâfunktioon. Myos toinen rivi
yhtàlôstâ (L2.11) voidaan kehittâa hiukan toisenlaiseen muotoon
1 X * ɔ
(l2∙13)s ∫ —≡=veχP(-τ-⅛--^ + x)a⅛ =
c j , σ√2τr7 2σ"/ 2
6 σ
" ɪog(- )-('ʃ-
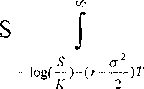
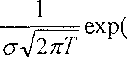
........-,r. (x~
2σ~T
- 2xσ2 T + σ4 T2 )]√x =
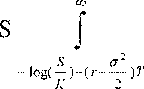
1 r (x-σ2Γ)21j
—7= exp [.. Их
σ-χ∣2πT 2σ2T
More intriguing information
1. Automatic Dream Sentiment Analysis2. Rent Dissipation in Chartered Recreational Fishing: Inside the Black Box
3. If our brains were simple, we would be too simple to understand them.
4. Wettbewerbs- und Industriepolitik - EU-Integration als Dritter Weg?
5. The name is absent
6. The name is absent
7. The name is absent
8. The name is absent
9. Enterpreneurship and problems of specialists training in Ukraine
10. Outline of a new approach to the nature of mind