Large-N and Large-T Properties of Panel Data Estimators and the Hausman Test

where A_k,l and a_k denote the (k, l)^th and the k^th elements of matrix A and vector
a, respectively. In view of (48) and (49) (the limits of N Pi I1,i,NTI1 i nt and
N ∑_i I2,i,NTI'₂,_i,N_τ), we can see that all of the elements in N ∑i I1,i,NTI'₂,_i,N_τ
converge to zero, except for

N X D32τ (^χ32,i ^- EFzi ^χ32,i) (EFzi ^χ32,i ^- EFz^χ32) D32T.

i

Thus, we can complete the proof by showing that this term converges in prob-
ability to a conformable zero matrix.

Let

Qι,iτ = D32τ (χ32,i — EFzi χ32,i) ;

Q2,iT = D32T (EFzi ^x32,i ^- EFz ^x32~) ';

Q2,i = H32 ^^g32,i (^zi) ^- N X ^g32,i (^zi) + μg32,i

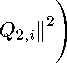
By the Cauchy-Schwarz inequality and Lemma 12,

N X Q1,iT (Q2,iT ^- Q2,i)'
i

(N X ^kQ^ι>i^τ∣∣²) (N X ^kQ2^,i^τ

^Ν X ^kQ1,iTliɔ ^sup ^kQ2,iT ^- Q2,ik2

Op(1)o(1)=op(1),

where the last line holds since

E(⅛ X kQ1,iTll²) <M
by Lemma 15(d) and by Assumption 6. Thus,
11

N    Q1,iTQ2,iT = N    Q1,iTQ2,i ^{+ o}P ⁽¹⁾ .

Next, notice that EQ1_,iTQ^'_2,i =0. Then, by the Cauchy-Schwarz inequality,

(N X ^vec (^Q1,iTQ2,i))
^N X ^(Q2,i ° ^Q1,iT))

N2 XhE kQ2,ik⁴ E kQ1,iTk4i 1/² .

i

43

<<   40   41   42   43   44   45   46   >>

More intriguing information