Notice that since ∣∣Z⅞τ (E⅛^χ3jit — Ex3jit) ∣∣4 ≤ τ (r)4 G (¾)4 by Assumption
6(iv), we have sup, ∣∣Z⅞feT (A¾y.⅛fe,i - Ex3kti) ∣∣4 ≤ (ʃθɪ τ (r)4 dr) supiG(¾)4
for к = 1,2, and 3. Therefore, by Lemma 10, we have
E KD3kτ (Ej^ix3k,i — Ex3k1i} K

(uniformly in i)
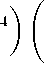
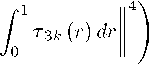
< ∞, for к = 1, 2, 3,
where τ3ι (r) = 0. So,
supE ∖∖D3τ (Eτz.x3,i - Ex3ji) ∣∣4 < ∞. (67)
Similarly, it follows that
sup sup E ∣∣Z⅛τ (E∏sx3 - E⅛)∣∣4 < ∞∙ (68)
N,T l<i<N
In addition, notice that
sup sup ∣∣Z⅛τ (Ex31i - Ex3)Il
N,Tl<i<N
sup sup
N,T l<i<N
(D33τ {Ex33tι — Ex33)
D3∙2τ (Ex321i — Ex32) — H32μg32i
D33τ {Ex33yι — Ex33) — H33μg33.
(69)
+ sup sup
N 3<i<N
0
-^32 At332
-^33 At333
By Assumption 6(v), as T → ∞,
sup sup
N 3<i<N
(D33τ (Ex33g. — Ex33)
D3,2τ (¾2,i — Ex32) — H32μg32 .
D33τ (Ex33ji — Ex33) — H33μg33 .
sup sup
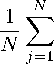
D33τ {Ex33,i — Ex33j) ''
D32τ (Ex32,i — Ex32j) — H32 (μg32 i — At3323J
D33τ (Ex33ιi — Ex33j) — H33 ∖μg33 i — μ933 j) J
sup
i,j
f D33τ (Ex33ji — Ex33j)
D32τ (Ex32,i — Ex32j) — H32 ∖μg32 i — At332i3
D33τ (Ex33,i — Ex33j) — H33 [μg33 i — μ933 j
46
More intriguing information
1. The name is absent2. Valuing Farm Financial Information
3. An alternative way to model merit good arguments
4. Evidence on the Determinants of Foreign Direct Investment: The Case of Three European Regions
5. Voluntary Teaming and Effort
6. Knowledge, Innovation and Agglomeration - regionalized multiple indicators and evidence from Brazil
7. THE INTERNATIONAL OUTLOOK FOR U.S. TOBACCO
8. Are class size differences related to pupils’ educational progress and classroom processes? Findings from the Institute of Education Class Size Study of children aged 5-7 Years
9. The name is absent
10. CAPACITAÇÃO GERENCIAL DE AGRICULTORES FAMILIARES: UMA PROPOSTA METODOLÓGICA DE EXTENSÃO RURAL