Expected outcome of reflection = Pref- ■ G - Cref (i)
The strategy with the highest expected outcome will of
course be chosen. In these equations G, Csearch and Pref
are constants, but Psearch(i) and Cref(i) will vary in time.
The chance that search will reach the goal is dependent on
the amount of knowledge and the current evaluation of this
knowledge:
L1(i)P1(i) + wL2(i)P2(i)
P (i) =
search() = --------------L 1--(---i--) + w L---2---(--i---)--------------
The w constant determines how much more useful higher-
order knowledge is with respect to basic knowledge. P1 (i) is
the contribution to the chance of success of level 1 knowl-
edge, and P2(i) the contribution of level 2 knowledge. The
chances of success increase as knowledge increases, but
decrease over time if the goal is not reached. Both P1 (i) and
P2(i) can be calculated using:
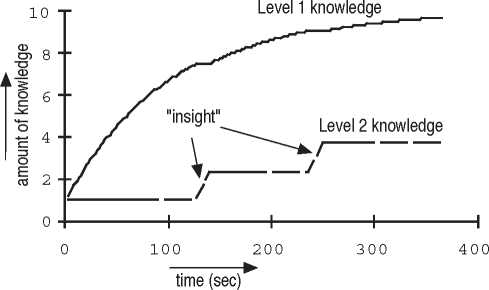
Figure 2: Value of level 1 and level 2 knowledge for G=20
Pj(i)
pdecay
Lj (i-I)' Pj (i —I) + Lj (i) — Lj (i —I)
Lj(i)
;(j=1,2)
pdecay represents the decay in chance of success, and has
typical values between 0.95 an 0.99 if the strategy in step i
was search and the goal hasn’t been reached. Otherwise
pdecay = 1 .
The cost of reflection depends on two factors: the cost is
higher if there is less basic knowledge, and the cost is higher
if there is already a lot of higher level knowledge:
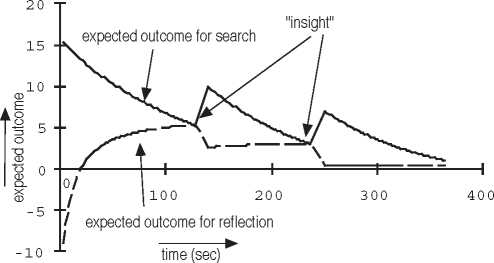
Figure 3: Evaluations of search and reflection for G=20
Cref(i) = Cbase +
( L1 max ^ ( L 2( i )ʌ
Ic ι∑m + (c 2L—J
L1 (i) L2max
Finally we have to say something about time, since we have
talked about “steps” in the previous discussion. Each step
takes an amount of time which can vary. So, following the
ACT-R intuition that cost and time are related to each other,
we take the estimated cost of the strategy at step i as the
amount of time step i takes:
T(i) = T(i—1)+C(i)
where C(i) is either Csearch or Cref(i), dependent on the
strategy at step i.
Results
If we choose appropriate constants and starting values for the
variables described above, we can calculate the increase in
knowledge over time. Note that the model assumes that the
goal is never reached, so the results simulate a subject that
never succeeds in reaching the goal. Figure 2 shows the
value of L1 and L2 with respect to T . The corresponding
evaluations for search and reflection are shown in figure 3.
At the start of the task, search is superior to reflection, but as
search fails to find the goal, and the basic (level 1) knowl-
edge increases, reflection becomes more and more attractive
up to the point (at T=127) where reflection wins from search.
Since reflection leads to an increase of level 2 knowledge,
search becomes again more attractive (using the newly
gained knowledge), and since the cost of reflection increases
with the amount of level 2 knowledge already present, reflec-
tion becomes less attractive. As a result search will again
dominate for a while, up to T=385 where reflection wins
again. We assume problem solving continues until both
expected outcomes drop below zero, since then neither strat-
egy has a positive expected outcome. In the example this is
the case at T=510.
Figure 2 and 3 show the results of the model for G=20. As
noted, G is the value of the goal. So using a lower value for
G corresponds to the fact that a subject values reaching the
goal less, or the fact that a subject is less motivated. If we
calculate the model for G=15 we get the results as depicted
in figure 4 and 5. The result is that reflection occurs only
once, and later (at T=203). Furthermore, at T=363 both eval-
uations drop below zero, so a less motivated individual gives
up earlier. If G is further decreased to 12, no reflection at all
takes place, and the give-up point is at T=237.
Discussion
The dynamic growth model nicely describes the phenomena
around insight in the literature and in our experiments. Fur-
thermore, it explains why this behavior is rational. It also
predicts changes in strategy due to motivational factors. It
however poses new questions. What is the nature of the basic
and higher-level knowledge? How will the model behave if
the goal is reached at some point? What mechanism is
responsible for gaining new knowledge, and how is it repre-
sented? The second model we will discuss in this paper will