4. Расчет величин разрывов для типичных распределений
4.1. Величина разрыва для равномерного распределения
Для равномерного распределения оценки вероятности имеем величину
разрыва Rrupture
+l 3
D(p)=∫p22ldp=2lp3
-l
+l 1 l3 1 l3
=+
l 2l 3 2l 3
l2
3
1 1 l 1 1 1 p2 +l 1 l2 l
Rrupture ( P ) ≡ - M1/2( P ) = “J P-,dP = =-l-Γ = ~:
2 20 l 2l 2 0 l4 4
R-npure ( p ) = __ 3з = √3
0.433 >1
3
DPp) 4 l 4
4.2. Величина разрыва для нормального распределения
Для нормального распределения оценки вероятности имеем
D(p) =σ2
2
1 1 +∞ 1 - — .
R—(p) ≡ 2M,/2(p)=2 ∫2p —e dp=
+∞
+∞
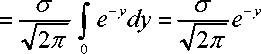
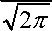
Rrupture (p) σ 1
Dd ( p ) 2∏σ σ
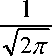
0.399>1
3
4.3. Величина разрыва для распределения Лапласа
Для распределения Лапласа оценки вероятности имеем
+∞
D(p)= Jp
21
dp = - p 2 e
-λ p
+∞
+∞
J2p 2 e-λ p dp =
= -0 + 2p e
2λ
+∞
+∞
+ J2 1 e
2λ
11
dp = + =
λ2 λ2
λ2
Rrupture(p)≡ 12M1/2(p)
+J∞pλe-λ p dp = 1 pe
02
+∞
+∞
Je-λ p dp =
20
=0+ 1 e-λ p
2λ
1
2λ
Rruptue(p) 1 λ 1
D(>(p) 2λ √2 2√2
≈ 0.354 > 1
3