A MARKOVIAN APPROXIMATED SOLUTION TO A PORTFOLIO MANAGEMENT PROBLEM

Fig. 20. Yield location and spread measures.

To quantify a risk level associated with this policy,
two popular risk measures, Valuc-at-Risk (VaR)
and Conditional Valuc-at-Risk¹⁵ (CVaR) can be
approximately calculated from the histogram. The
/J-VaR of a portfolio is the lowest- amount- a such
that, with probability β the loss will not- exceed
α; here

.9-VaR ≈ 30,000.

The /J-CVaR is the conditional expectation of
losses above the amount- α; here

.9-CVa-R. ≈ 34,000.

These measures disqualify the policy of maximis-
ing the expected yield as a fund manager’s ob-
jective function. No manager would accept- such a
high risk in controlling a pension fund.

A different- strategy has to be considered. Sup-
pose that the manager will use a “constrained”
strategy: t⅛_ιt = .5, U∙2,t = .02.τ_f (i.c., non optimal
with respect- to the expected value criterion). Wc
can see from Figure 21 (lower panel) that, for
the same initial outlay .τo = $40,000, the yield
distribution (represented by the light- histogram)
is more concentrated and less skewed than the
unconstrained one (upper panel). The mean for
this portfolio is $84,100 (mcdian=58,710) and the
standard deviation diminishes to $45,563 from
$168,000 for the unconstrained policy. The dark
histogram represents the final fund’s yield dis-
tribution for the constrained strategy applied to
.τo = 60,000. In this ease, the mean value is

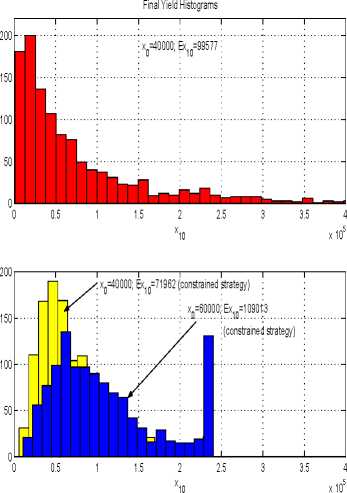
Fig. 21. Fund yield spread.

$109,013 (mcdian=93,000) and the standard de-
viation $63,322. Overall, the risk of performing
worse than investing in the secure asset- alone is
much less under a constrained strategy. The risk
of scoring less than .τ₀ is, for .τ₀ = 40,000

.9-VaR ≈ 13,000 and .9-CVaR ≈ 17,000;

whereas for .τ₀ = 60,000,

.9-VaR ≈ 21,000 and .9-CVaR ≈ 30,000.

Suppose now that the fund manager would like to
advertise their pension fund as paying an amount
Xτ for an initial outlay .tq∙¹⁶ It is clear from
the histograms in Figure 21 that an expected
value maximisation policy (constrained or not)
cannot- be used for this purpose. Instead, we will
examine the policy determined as a solution to
the stochastic optimal control problem with the
objective function given as

J(0,.τ(0)ρu) =IE ^7r(.ττ)∣ .τ(0) = .τo^ (37)
where

₁ ( x ʃ (∙'fτ -⅛)⁵ if xτ > xτ■ ∕o₈∖

This criterion reflects the manager’s wish to dis-
pose of sufficient- funds to meet- the target- xτ∙ At
the same time, it- docs not- prompt- the manager to
accumulate (much) more than needed.

¹⁵Soo [1] for a static portfolio analysis based on VaR and
Cλ^raR.

¹⁰In other words, the manager will sell a ten year “bond⁷’
Sio fɑɪ' -ro-

<<   11   12   13   14   15   16   >>

More intriguing information