A MARKOVIAN APPROXIMATED SOLUTION TO A PORTFOLIO MANAGEMENT PROBLEM

1.2

1

at the constraint. However, this does not affect
the consumption strategy. The new discounted
total utility is 717 and the standard deviation
equals 108, which is substantially less than un-
der the unconstrained regime. The wealth and
strategy sample paths are shown in Figure 18.
The conservative investment strategy results in
much less “volatility” in consumption and wealth
as observed by eye and measured by the utility
standard deviation.

0.4

0.2

0.8

м

= 0.6

2

4

6

8

10

0

wealth                                      χi0⁴

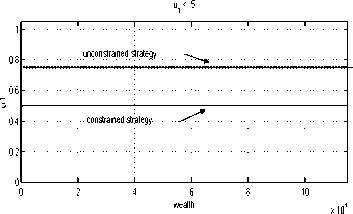
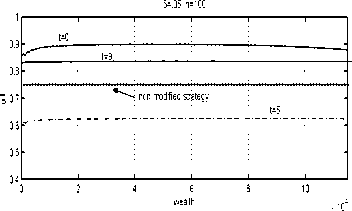
Fig. 15. Cosine modified strategies.

x 10⁴

Cosine modifies realisations

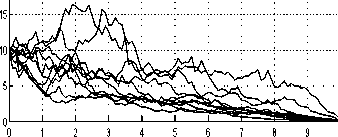
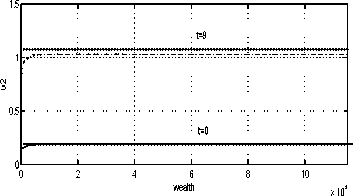
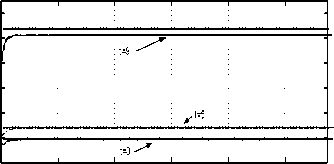
Fig. 17. Constrained strategies.

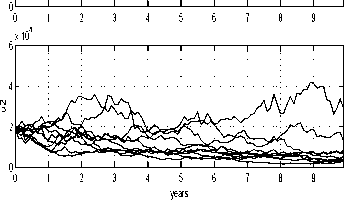
Fig. 16. Cosine modified realisation paths.

5.2 Constrained Policies

1∣-........!.........!.........!.........■.........!.........!.........■.........I

= 0.5---------------:----------------:----------------`----------------`----------------:----------------`----------------`-----------------

A portfolio manager might have an a, priori belief
that their investment should not exceed a certain
wealth percentage. Such a constraint can easily be
allowed for in the above numerical optimisation
procedure.

Suppose that the permissible investment level is
Ui = .5. Figure 17 reveals the modified strategy.
Not surprisingly, the agent is expected to invest

0---------------------1---------------------1---------------------∣---------------------1---------------------1---------------------1---------------------1---------------------1---------------------L

0          1          2         3         4         5         6         7         8         9

x 10⁴

61---------------------1---------------------1---------------------1---------------------1---------------------1---------------------1---------------------1---------------------1---------------------Γ

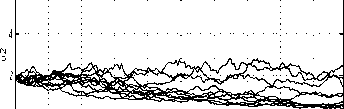
0∣---------------------1---------------------1---------------------1---------------------1---------------------1---------------------1---------------------1---------------------1---------------------L

0          1          2         3         4         5         6         7         8         9

Fig. 18. Constrained strategy realisation paths.

12