The name is absent



27

3.2.1 BS-mallin Ominaisundet

Kaavoissa (8) ja (8)’ esitettiin eri muuttujien Vaikutussuunnat option hintaan plus- ja
miinusmerkkien avulla. Seuraavassa tarkastellaan BS-шаШп Ominaisuuksia suhteessa osto-
optioon hieman yksityiskohtaisemmin eraiden Osittaisderivaattojenja raja-arvojen muodossa.

3.2.1.1 BS-mallin Osittaisderivaatat suhteessa kohde-etuuden hintaan, Iunastushintaanja
maturiteettiin osto-option tapauksessa.

Osto-option hinnan Osittaisderivaatta suhteessa kohde-etuuden hintaan eli option delta-arvo

(Δ) , voidaan esittââ seuraavasti

-lr        ln(S / K)+[r-(--)](T-t)]

(15) —ɪ =SW------------2------ > o42

∂S

Kohde-etuuden hinnan nousu siis nostaa osto-option hintaa. Kyseisen Osittaisderivaatan
kâanteisluku, l∕∆, on option Suojautumiskerroin (hedge ratio), joka ilmaisee, kuinka monta
asetettua optiota meidan tulee yhdistâa yhteen kappaleeseen ostettua kohde-etuutta, jotta
muodostamme portfolio olisi tâysin Suojattu.


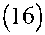
In(S∕X') + l>∙-(⅛7'→)]
■----------------2--------- ,<0

∂Cbs = c-'V-∣in
∂K


σjτ~t

ln(S∕∕O + [r-(-y-)](T→)]



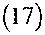
∂(T-t)


σ-Jτ~t

σ    πin(S∕Λ∙) + [r-(-)](T-r)]

—-  ..:     ---------. > O , n= normaalijakauman tiheysfunktio

2y∣Y-t           σ-jτ~~t
42 Tassa yhteydessa tyydytâan ainoastaan esittamâan kyseiset Osittaisderivaatat, jotka
Itseasiassa ovat melko tyôlaitâ johtaa, mutta apuna voidaan kâyttâa tietoa, ettâ Standardoidun
normaalijakauman kertymâfunktion derivaatta on sen tiheysfunktio. Osittaisderivaattojen
tarkemmasta johtamisesta, ks. esim Vauramo (1993, Iiitel)



More intriguing information

1. The name is absent
2. The Global Dimension to Fiscal Sustainability
3. Trade and Empire, 1700-1870
4. A Theoretical Growth Model for Ireland
5. Income Taxation when Markets are Incomplete
6. Fertility in Developing Countries
7. The name is absent
8. PROTECTING CONTRACT GROWERS OF BROILER CHICKEN INDUSTRY
9. The name is absent
10. The name is absent